[NOTICE] 本文仅为一篇我个人学习笔记，不适合作为其他人的学习引导。

因为博主写这篇笔记就是这个状态 ↓

↑ 为此专门查了怎么用more标签隐藏文章内容

前言

为啥搞这？吃饭

这大概是我写过最粗暴的前言了 (

注：我在写这篇笔记时尚未学习高数II、大物和离散数学，所述内容可能存在错误。

为啥可以对图像进行分析呢？

在 RGB 模型下，不谈 Alpha 通道，图像上所呈现的每一个像素点，都是 RGB 三个通道各自取不同的值然后叠加形成的。
通常每个通道的取值范围为 0~255 (2^8-1)。若单独研究一个图像的一行像素，以横坐标为像素点位置，纵坐标为通道值绘制出来，会发现一个神奇的现象：

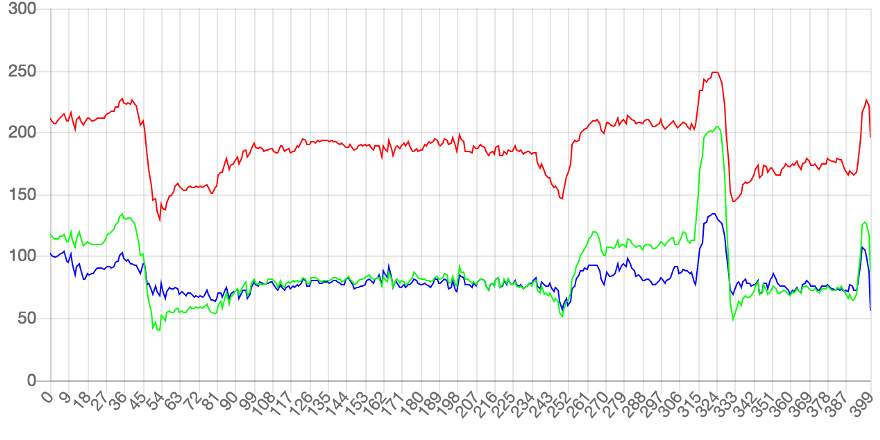
可以看到，每条曲线都在不停的上下波动。但是有些区域的波动比较小，若将，曲线波动较大的地方，正是图像内容出现显著改变的地方。

显然，波动与图像是紧密关联的。不难得出，图像由一组波组成的。

图像滤波

物理学的滤波

总的来说，滤波分为高通滤波和低通滤波。
这和物理学的滤波没差，即分别为：

高通滤波(highpass)：容许高频信号通过，但减弱（或减少）频率低于截止频率的信号的通过
低通滤波(lowpass)：容许低频信号通过，但减弱（或减少）频率高于截止频率的信号的通过

滤波的典型应用就是高音和低音喇叭了，假设一个简单的音调仅由一个高频音和一个低频音合成。通过高通和低通滤波，可以将合成后的音调(波)拆分出与原始音调(波)完全相同的高频和低频波，然后将滤出的分别送往高音喇叭和低音喇叭播出声音。

图像的滤波

“曲线波动较大的地方，正是图像内容出现显著改变的地方”，不难想出：

如果我们将低通滤波应用于图像的波，将会使图像的色彩变化剧烈的地方被“磨平”，也就是让变化变得平滑，产生俗称 “撸多了” 的效果
如果我们将高通滤波应用于图像的波，将会使图像的色彩变化不大的地方将失去，也就是只有变化剧烈的地方才会留下来，产物大概就是线稿

提取图像边缘/图像的求导

不难想出，可以用高通滤波来对图像进行处理，使其中的变化剧烈的的区域留下。
然而，说是这么说，直接拿这一套对于图像处理可能就出问题了：

由于实际景物图像的边缘往往是各种类型的边缘及它们模糊化后结果的组合，且实际图像信号存在着噪声。噪声和边缘都属于高频信号，很难用频带做取舍

不妨换一种思路，可以知道，图像可以看作一个二维的离散数集。
而如果将求导(有限差分)应用于这个数集，就可以得到此处的变化率，再比较，进而可以进行滤波。

有一些常见的边缘检测算法可以解决这个问题：
典型的是 Roberts算子，它是一种利用局部差分算子寻找边缘的算子，它给出公式:

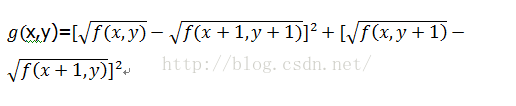
其中 f(x,y) f(x+1,y) f(x,y+1) f(x+1,y+1) 分别为4领域的坐标，且是具有整数像素坐标的输人图像;其中的平方根运算使得该处理类似于人类视觉系统中发生的过程。

[算子(Operator) 是将一个元素在向量空间（或模）中转换为另一个元素的映射]

啊等一下，先看看用中心差分来找边缘吧


Mat src = imread("test.jpg", 1);
cvtColor(src, src,COLOR_BGR2GRAY); //转换为灰度图像
//C1: Single Channel
namedWindow("src", WINDOW_AUTOSIZE);
imshow("src", src);

Mat dImg = Mat(src.rows, src.cols - 2, CV_8UC1); //C1: 单通道
//显然中心差分运算会导致结果的两个列丢失
for (int i = 0; i < src.rows; i++) {
    for(int j = 1; j < src.cols - 1; j++) { //这里对列进行中心差分运算
        dImg.at<uchar>(i, j - 1) = src.at<uchar>(i, j + 1)
        - src.at<uchar>(i , j - 1);  //中心差分g(x) = f(x + 1) – f(x - 1) 
    }
}
namedWindow("dst", WINDOW_AUTOSIZE);
imshow("dst", dImg);

为啥要转换成灰度图像啊

自然界中，颜色本身非常容易受到光照的影响，RGB变化很大，反而梯度信息能提供更本质的信息

三通道转为一通道后，运算量大大减少

opencv的很多函数只支持单通道

然后就可以得到和下图一样烂的边缘描绘（~~人体描边鬼才~~）了：

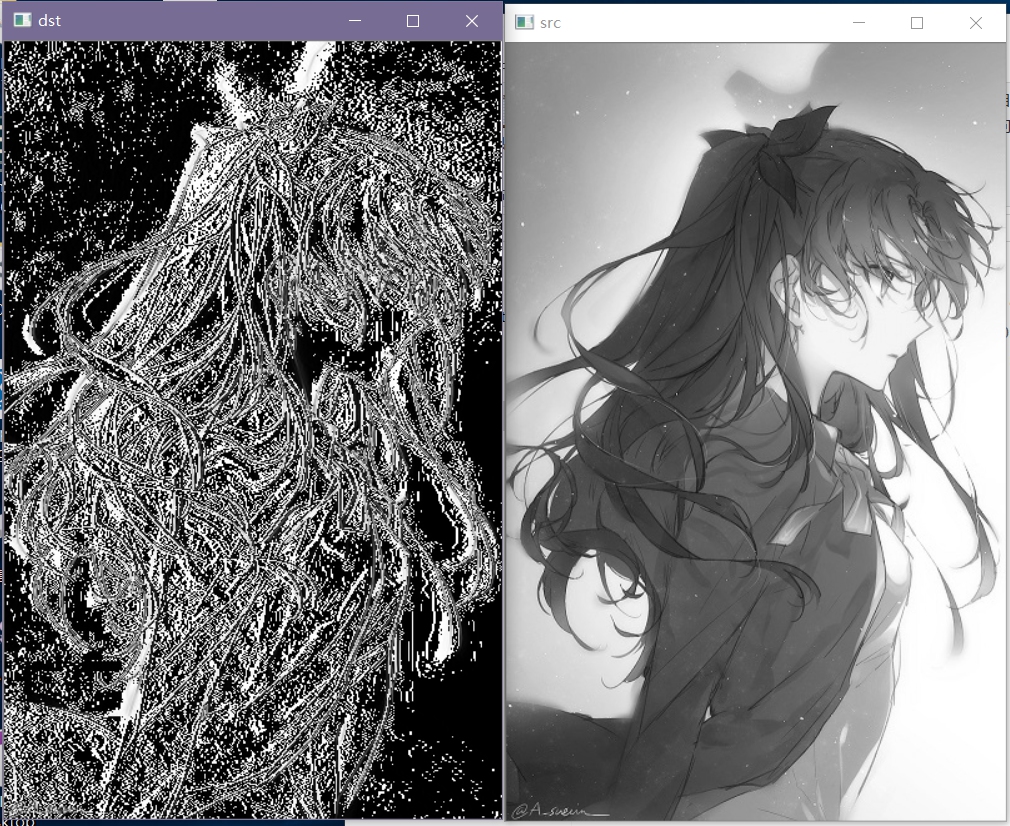
↑ 可以看到上图噪点（虽然并不）带来的影响是十分显著的

这就是为何要使用 Roberts算子 了：

Mat roberts(Mat srcImage) {
    Mat dstImage = srcImage.clone();
    int nRows = dstImage.rows;
    int nCols = dstImage.cols;
    for (int i = 0; i < nRows-1; i++) {
        for (int j = 0; j < nCols-1; j++) {
            int t1 = (srcImage.at<uchar>(i, j) - srcImage.at<uchar>(i+1, j+1)) *
                        (srcImage.at<uchar>(i, j) - srcImage.at<uchar>(i+1, j+1));
            int t2 = (srcImage.at<uchar>(i+1, j) - srcImage.at<uchar>(i, j+1)) *
                        (srcImage.at<uchar>(i+1, j) - srcImage.at<uchar>(i, j+1));
            dstImage.at<uchar>(i, j) = (uchar)sqrt(t1 + t2);
        }
    }
    return dstImage;    
}


int main(int argc, char* argv[]) {
    Mat src = imread("D:/test.jpg", 1);
    cvtColor(src, src,COLOR_BGR2GRAY);

    namedWindow("src", WINDOW_AUTOSIZE);
    imshow("src", src);

    Mat dImg = roberts(src);
    namedWindow("dst", WINDOW_AUTOSIZE);
    imshow("dst", dImg);
}

可以看到结果有非常明显的改善，几乎和线稿差不多了：

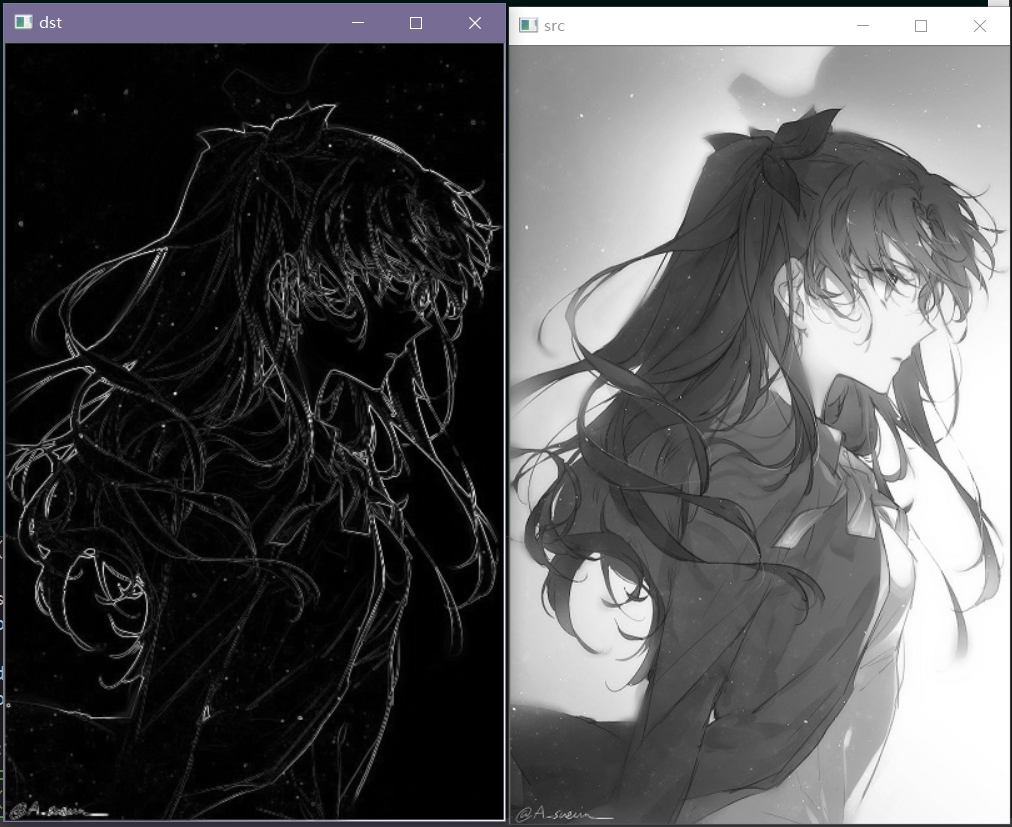
矩阵的卷积运算

假设输入信号为x[m,n]，激活响应为h[m,n]，则其卷积定义为：

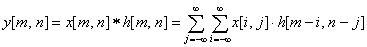
在图像处理中，激活响应（也称为核）h[m,n]通常是一个 3x3矩阵，其下标如下图所示

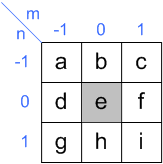
注意到原点 e(0,0) 是矩阵的中心。

矩阵的卷积运算可以简化为以下过程：

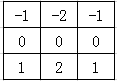
假设卷积核H:

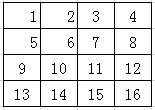
有一个待处理矩阵X:

要计算H,X的卷积A，首先应将卷积核以原点翻转 180°，即：

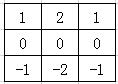
然后，将翻转后的卷积核H的原点对准X的第1行、第1列的元素 H₁₁，将对应元素相乘，没有元素的地方视为乘以0：

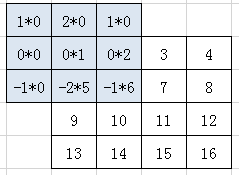
将如图所示蓝色区域的乘积结果相加，得到输出矩阵 A₁₁ 的第1行、第1列的元素的值 -16

将翻转后的卷积核H的原点对准X的第1行、第2列的元素 H₁₂，仍作这种运算，即：

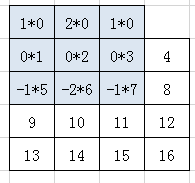
可得输出矩阵 A₁₂ 的值，以此类推，可得输出矩阵A。

对于 5x5 的卷积核(左蓝)、1x5 的卷积核(右蓝)、5x1 的卷积核(右绿)，仍有这种运算：

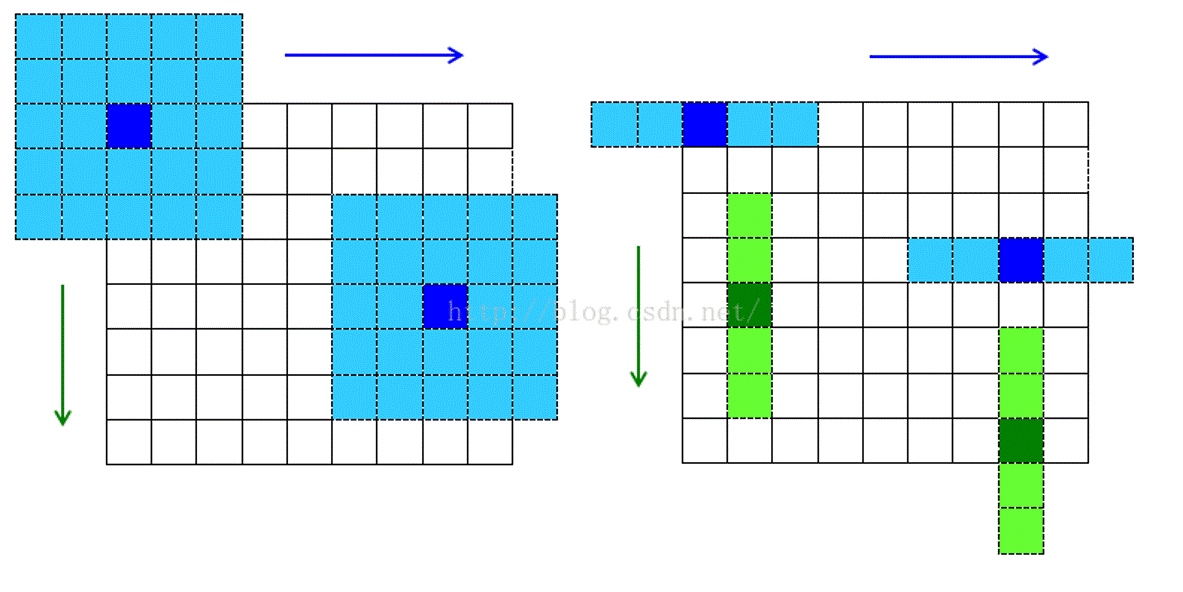
这种东西劲爆的地方就是，手算算不来，码代码也码不出来

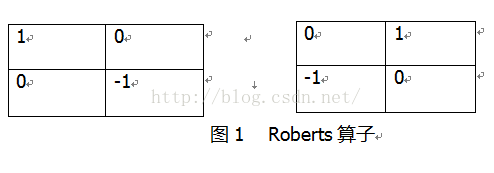
Roberts算子是2X2算子模板。下图所示的2个卷积核形成了Roberts算子。图像中的每一个点都用这2个核做卷积。

高斯模糊

高斯模糊可以简单理解为图像中的每个像素都重新设置像素值为周边相邻像素的加权平均值。
而这个 “相邻像素” 的范围越广，模糊程度越大。

这里使用正态分布进行加权处理：

根据公式，易得代码：

int main(int argc, char* argv[]) {

    Mat src = imread("test.jpg", 1);
    cvtColor(src, src,COLOR_BGR2GRAY);

    namedWindow("src", WINDOW_AUTOSIZE);
    imshow("src", src);


    //5x5卷积模版 
    Mat model = Mat(5, 5, CV_64FC1); //每行均为double

    double sigma = 80; //超参数 根据经验的初始参数，一个定值（哪个最吼）
    for (int i = -2; i <= 2; i++) { //5x5 矩阵,令卷积核为原点
        for (int a = -2; a <= 2; a++) {
            //?+2: cnm的数组没负的下标
            model.at<double>(i + 2, a + 2) =
                exp(-(i * i + a * a) / (2 * sigma * sigma)) /
                (2 * PI * sigma * sigma); //exp(x) = e^x
        }
    }

    double gaussSum = 0;
    gaussSum = sum(model).val[0];
    for (int i = 0; i < model.rows; i++) {
        for (int a = 0; a < 5; a++) {
            model.at<double>(i,a) = model.at<double>(i,a)/gaussSum;
        }
    }

    Mat dst = Mat(src.rows - 4, src.cols - 4, CV_8UC1);

    for(int i = 2; i < src.rows - 2; i++) {
        for(int a = 2; a < src.cols - 2; a++) {
            double sum = 0;
            for(int m = 0; m < model.rows; m++) {
                for(int n = 0; n < model.cols; n++) {
                    sum += (double)src.at<uchar>(i+m-2, a+n-2) * model.at<double>(m,n);
                }
            }

            dst.at<uchar>(i-2,a-2) = sum;
        }
    }

    namedWindow("gauss", WINDOW_AUTOSIZE);
    imshow("gauss", dst);


    waitKey(0);
    return 0;
}

文章目录

文章归档

分类目录

计算机幻觉从入门到入土

前言